株式会社ランスモアのホームページへようこそ。

No.570 ボールジョイント用ゴム製ダストカバーの軸圧縮変形解析における静的陰解法と動的陽解法の比較

　下記の文献を参考にして、解析モデルを作成し、LS-DYNAの静的陰解法と動的陽解法でそれぞれ接触解析を行った解析例を示します。

解析モデルは、3次元フルモデルとして作成しました。モデルの寸法は参考文献に記載の寸法を参照して作成しました。

Fig.1からFig.3にモデル図を示します。

圧子部分とダストカバー部分について、要素はすべて六面体一点積分ソリッド要素を用いてメッシュを作成しました。

駆動条件は、圧子に強制変位条件 8.0mm を与えました。

　本問題を、ANSYS LS-DYNAの動的陽解法(Dynamic Explicit)と静的陰解法(Static Implicit)による2つの解析手法を用いて解析し、ミーゼスの相当応力および最大主応力分布を比較しました。

Fig.5とFig.6に、強制変位 8.0mm を与えた時点における動的陽解法と静的陰解法でそれぞれ得られたミーゼスの相当応力分布を示します。両者はほぼ同じ応力分布をしており結果は一致しています。

Fig.7とFig.8に、強制変位 8.0mm を与えた時点における動的陽解法と静的陰解法でそれぞれ得られたミーゼスの相当応力分布を示します。ここではモデルの断面をカットして1/4モデルのように表示してダストカバー内部の様子がわかるように可視化しました。

Fig.9とFig.10に、強制変位 8.0mm を与えた時点における動的陽解法と静的陰解法でそれぞれ得られた最大主応力分布を示します。両者はほぼ同じ応力分布を示しており、動的陽解法と静的陰解法の解析結果は一致していると言えます。

Fig.11とFig.12に、強制変位 8.0mm を与えた時点における動的陽解法と静的陰解法でそれぞれ得られたミーゼスの相当応力分布を示します。

以上の比較より、本解析例では、動的陽解法の結果と、静的陰解法の結果はおおむね一致したと判断しました。

なお，本事例はサンプルであることをご了承下さい。

参考文献：境 真太郎、大林新一 :エラストマーの大変形FEM解析について, KOYO Engineering Journal No.156(1999)

Keywords: ゴム, ダストカバー，軸圧縮変形，FEM解析

Tools: LS-PrePost ver.4.11, LS-DYNA MPP Win64 R16.0

October 25, 2025 create a new entry

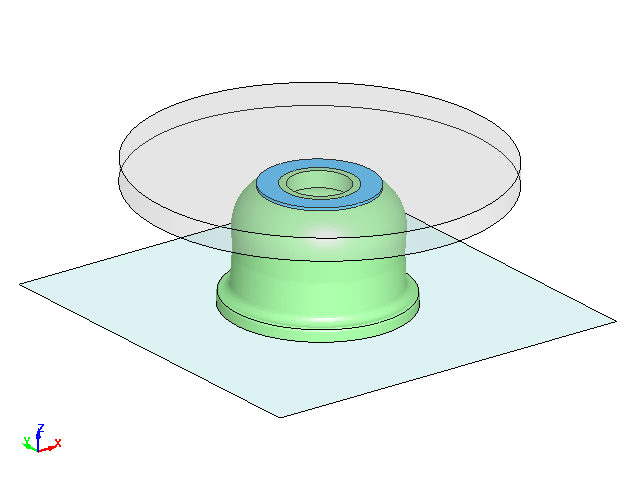
Fig.1 解析モデル図1

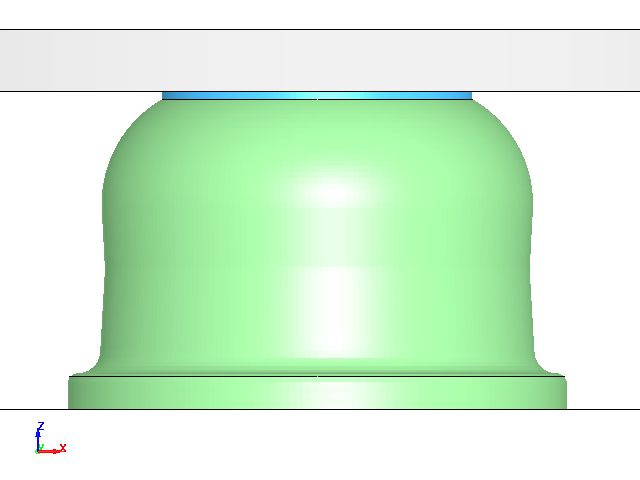
Fig.2 解析モデル図2

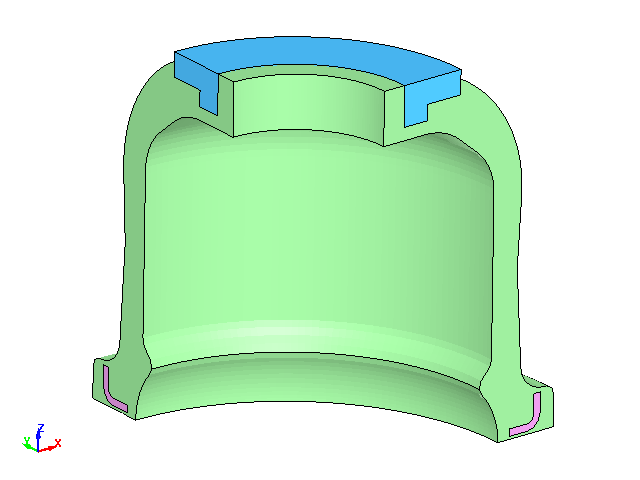
Fig.3 解析モデル図3

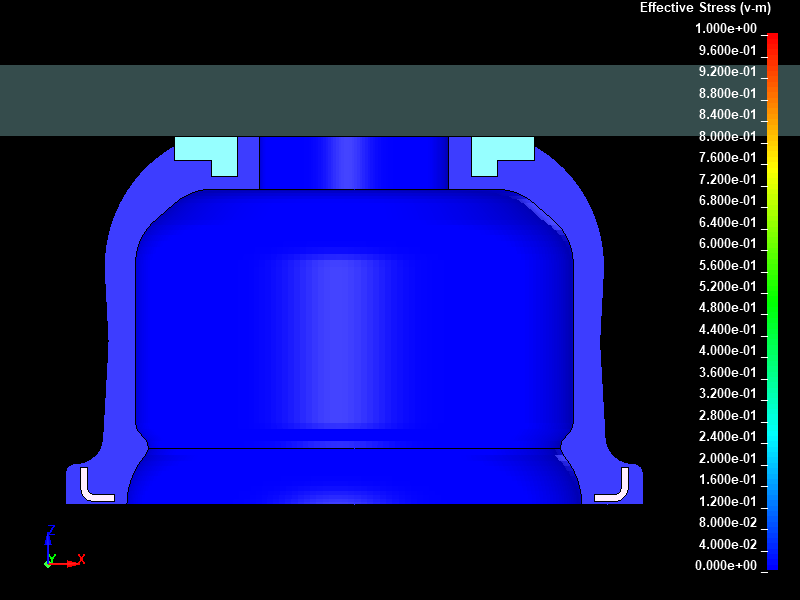
Fig.4 動的陽解法/ミーゼスの相当応力分布図/変形前/固定レンジ表示(0.0 to 1.0 MPa)

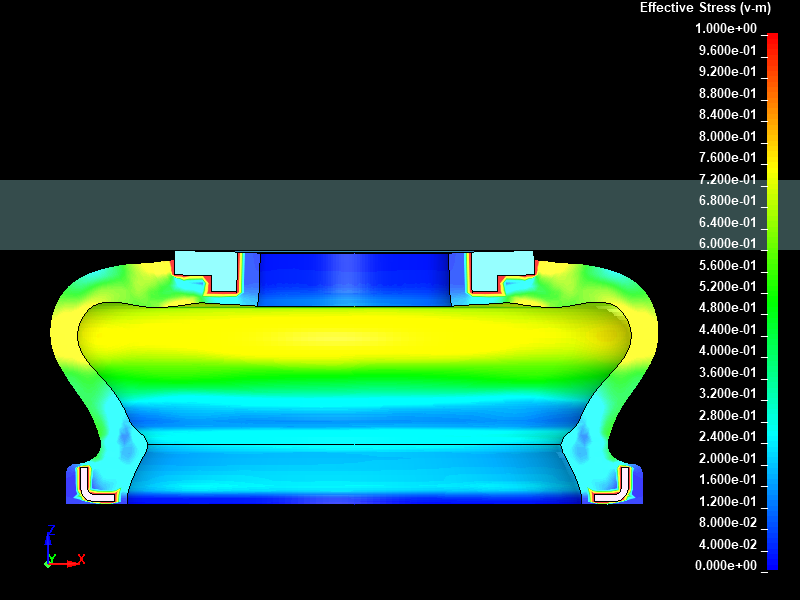
Fig.5 動的陽解法/ミーゼスの相当応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

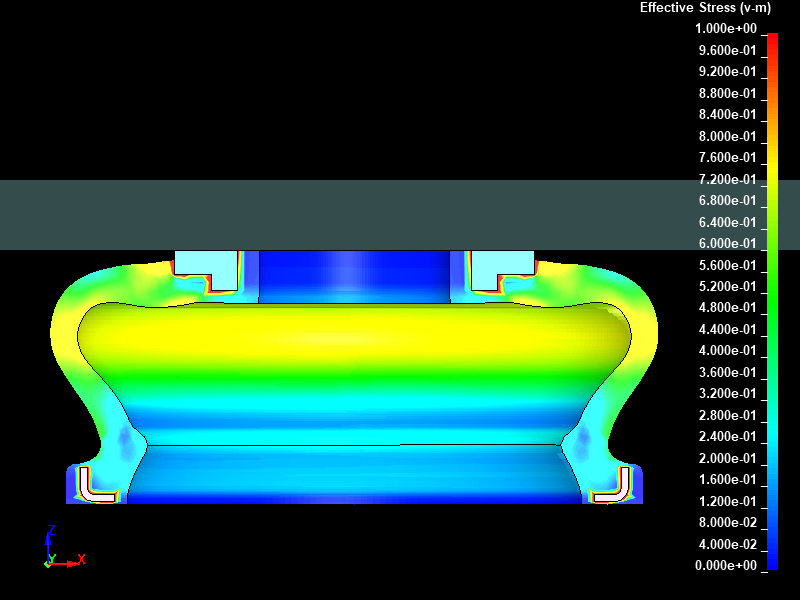
Fig.6 静的陰解法/ミーゼスの相当応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

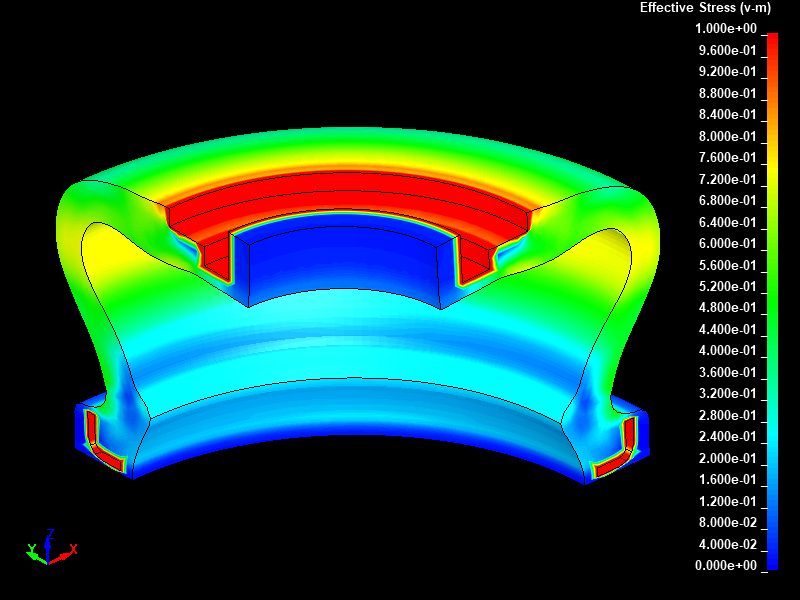
Fig.7 動的陽解法/ミーゼスの相当応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

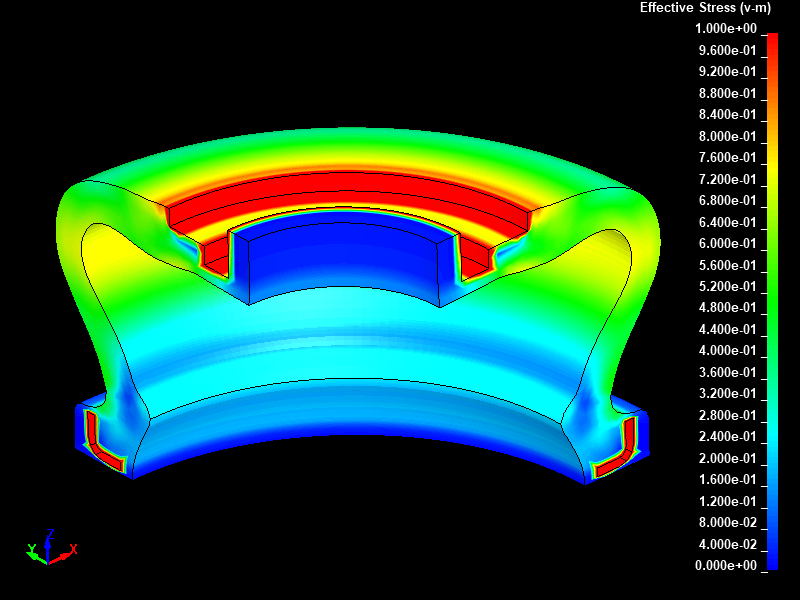
Fig.8 静的陰解法/ミーゼスの相当応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

Fig.9 動的陽解法/最大主応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

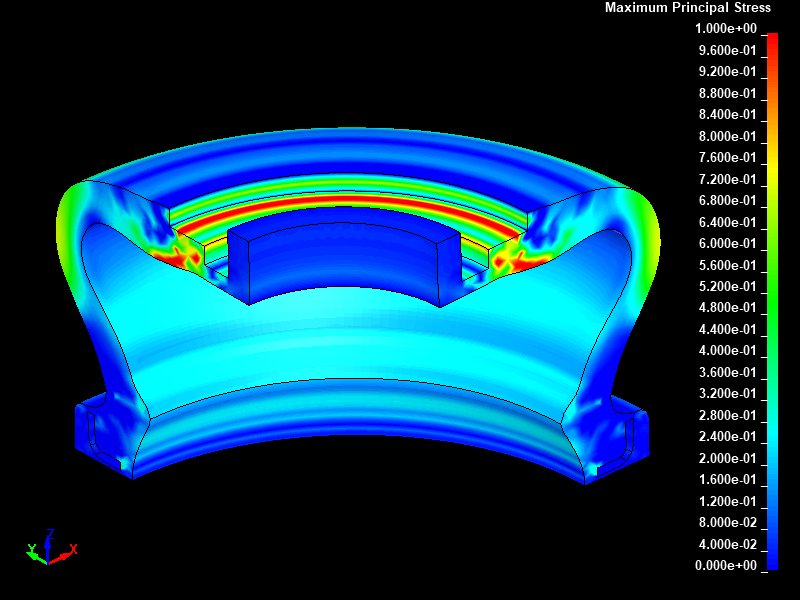
Fig.10 静的陰解法/最大主応力分布図分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

Fig.11 動的陽解法/ミーゼスの相当応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)

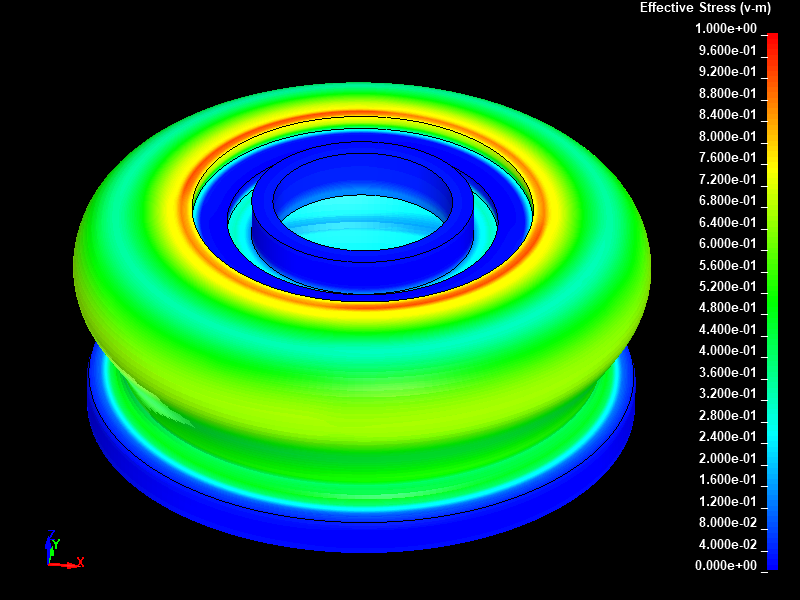
Fig.12 静的陰解法/ミーゼスの相当応力分布図/ストローク 8mm 変形後/固定レンジ表示(0.0 to 1.0 MPa)