株式会社ランスモアのホームページへようこそ。

No.563 引張を受ける孔あき鋼板の応力集中解析

　下記の文献を参考にして、解析モデルを作成し、LS-DYNAの静的陰解法により応力解析を行った解析例を示します。応力集中の問題に対して、メッシュ分割数とミーゼスの相当応力の最大値の関係を整理しました。

参考文献：岸 正彦 :例題で学ぶ有限要素法応力解析のノウハウ, 森北出版, p.135, 6.3 引張を受ける孔あき板2, 2008

Case001は、文献に記載されている方法でメッシュを作成して解析したケースです。
Case002は、Case001の2倍に分割数を増やしたケースです。
Case003は、Case002の2倍に分割数を増やしたケースです。(Case001に対して4倍に分割数を増やしたケースに相当)
Case004は、Case003の2倍に分割数を増やしたケースです。(Case001に対して8倍に分割数を増やしたケースに相当)
Case005は、Case004の2倍に分割数を増やしたケースです。(Case001に対して16倍に分割数を増やしたケースに相当)
Case006は、Case005の2倍に分割数を増やしたケースです。(Case001に対して32倍に分割数を増やしたケースに相当)

Fig.1 Case001のメッシュ分割図

Fig.2 Case002のメッシュ分割図

Fig.3 Case003のメッシュ分割図

Fig.4 Case004のメッシュ分割図

Fig.5 Case005のメッシュ分割図

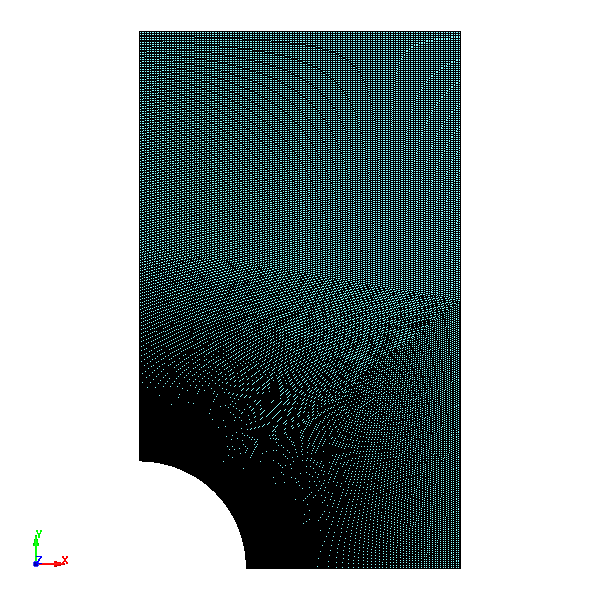
Fig.6 Case006のメッシュ分割図

Fig.7 Case001のメッシュ分割図 拡大図

Fig.8 Case002のメッシュ分割図 拡大図

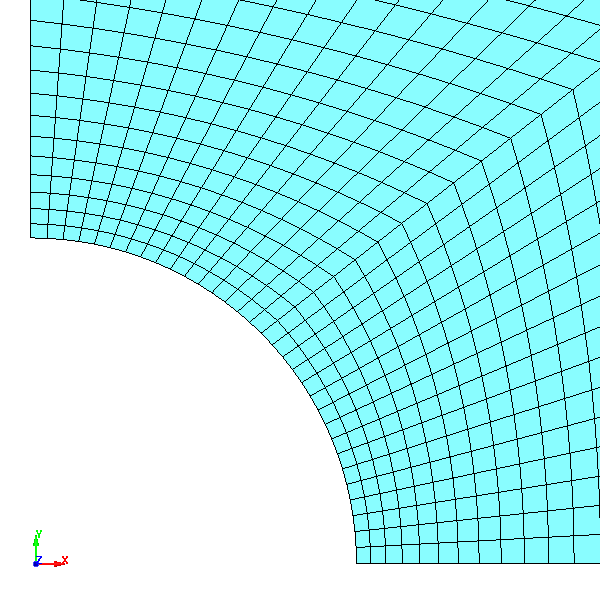
Fig.9 Case003のメッシュ分割図 拡大図

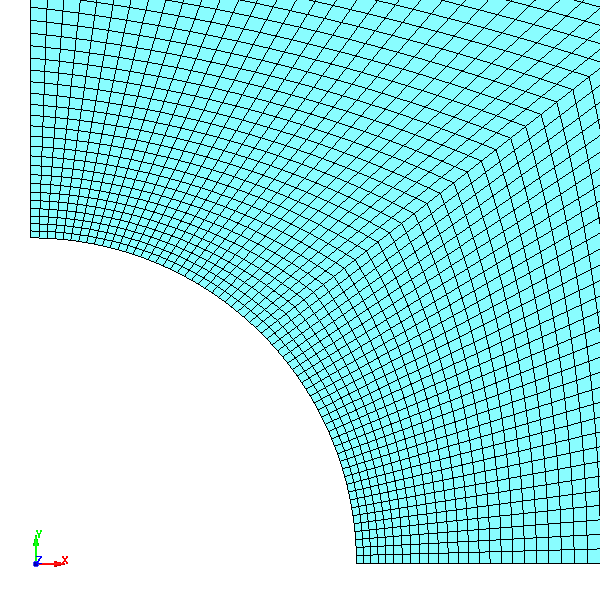
Fig.10 Case004のメッシュ分割図 拡大図

Fig.11 Case005のメッシュ分割図 拡大図

Fig.12 Case006のメッシュ分割図 拡大図

　本解析例は、LS-DYNAの静的陰解法を用いて解析を行いました。モデルは4分の１モデルとし、モデル上端に文献記載の荷重を上方向へ負荷しました。鋼板は線形弾性体でモデル化し、要素タイプは、完全積分タイプELFORM16のシェル要素でモデル化しました。線形弾性体の解析では、ある負荷荷重に対して応力集中に注目します。有限要素法における応力の値は、要素分割という空間解像度に依存します。分割数を増やすということは、メッシュ分割を細かくするということであり、それは解像度を向上させることになります。解像度が良くなれば、より詳細な変化を知ることができます。しかし、その代償として、要素数が増えるためメモリ使用量の増加と計算時間の増加というデメリットが制約条件として立ち塞がってきます。このメリットとデメリットをトレードオフして解析作業を進める必要があります。

なお，本事例はサンプルであることをご了承下さい。

Keywords: 孔あき鋼板, 引張解析, 応力集中, メッシュ分割, 解像度

Tools: LS-PrePost ver.4.11, LS-DYNA MPP Win64 R14.1

June 29, 2025 create a new entry

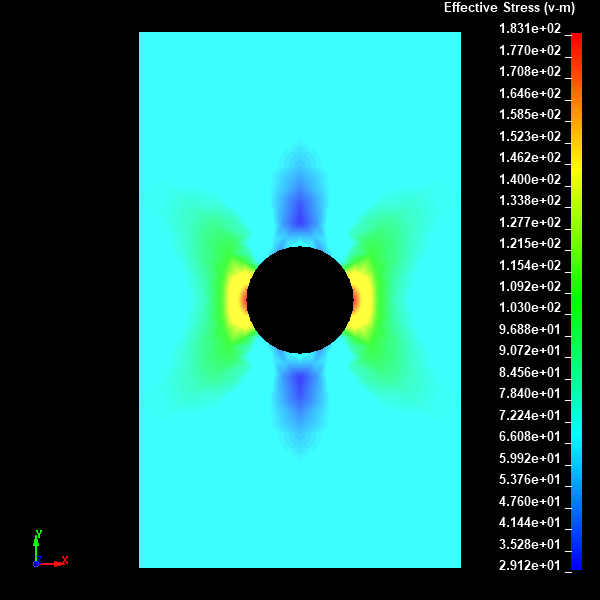
Fig.13 Case001のミーゼスの相当応力分布図(Nodal表示)

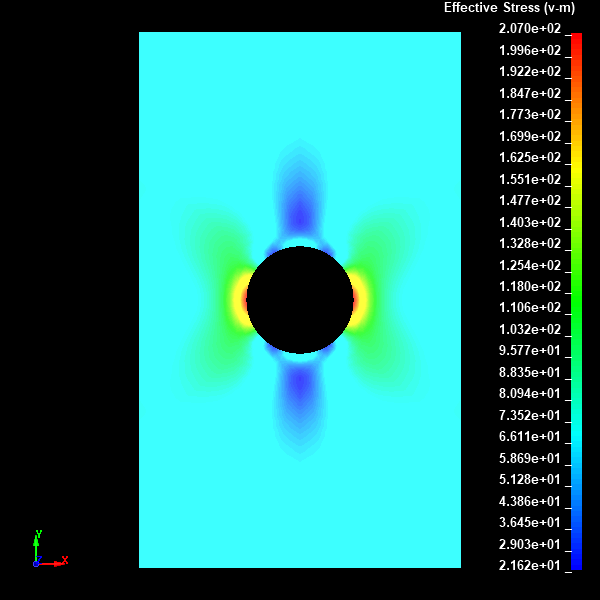
Fig.14 Case002のミーゼスの相当応力分布図(Nodal表示)

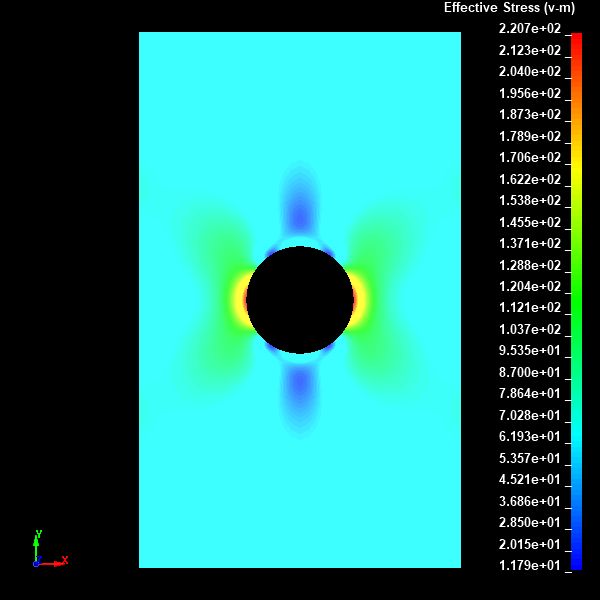
Fig.15 Case003のミーゼスの相当応力分布図(Nodal表示)

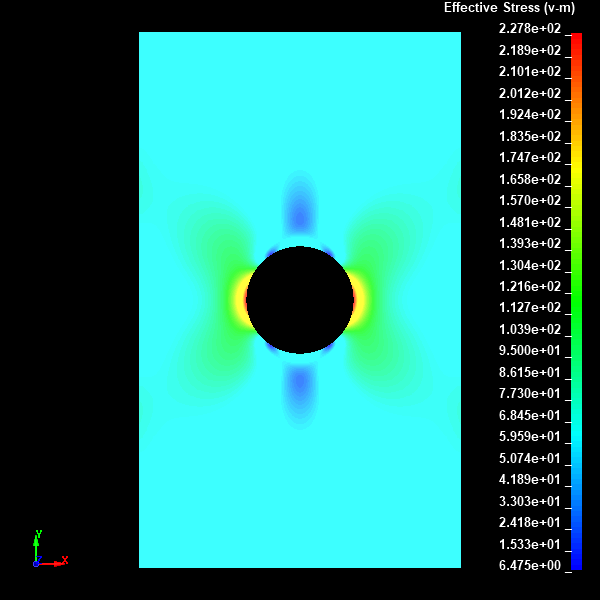
Fig.16 Case004のミーゼスの相当応力分布図(Nodal表示)

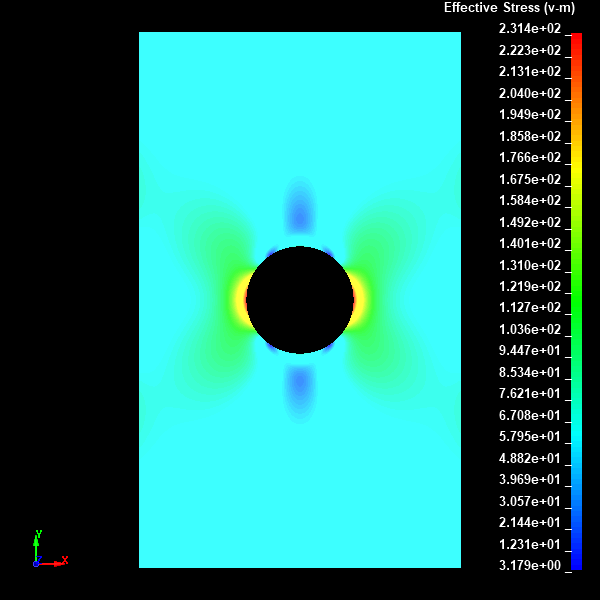
Fig.17 Case005のミーゼスの相当応力分布図(Nodal表示)

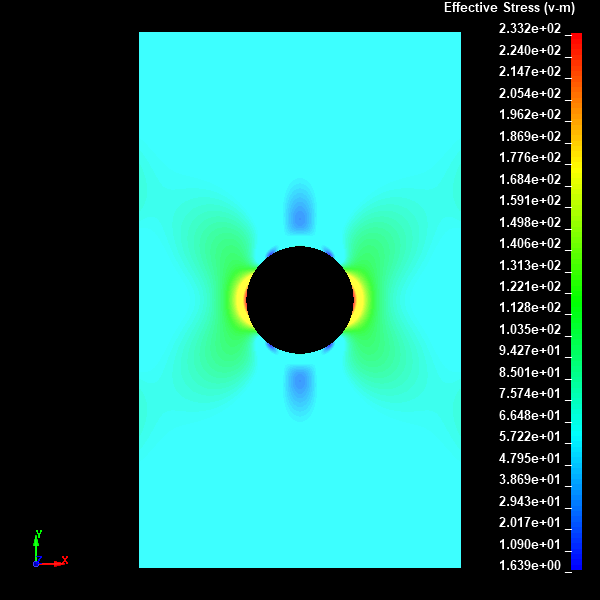
Fig.18 Case006のミーゼスの相当応力分布図(Nodal表示)

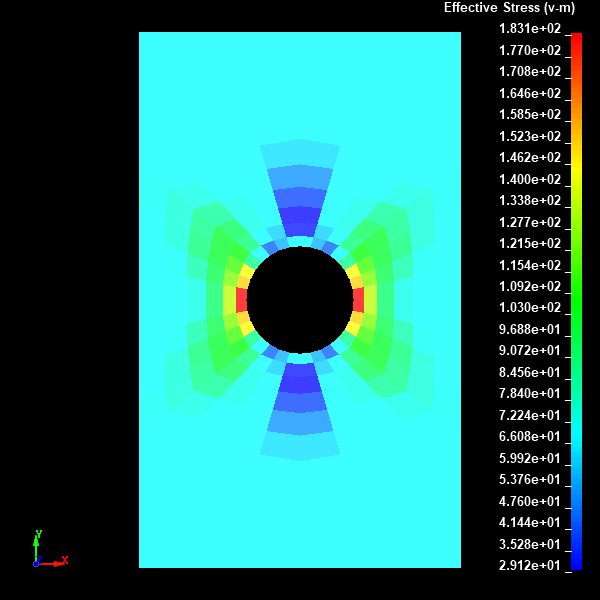
Fig.19 Case001のミーゼスの相当応力分布図(None表示)

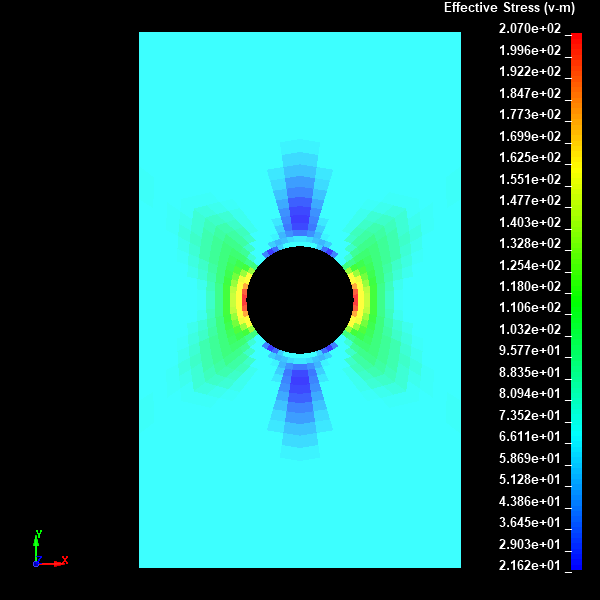
Fig.20 Case002のミーゼスの相当応力分布図(None表示)

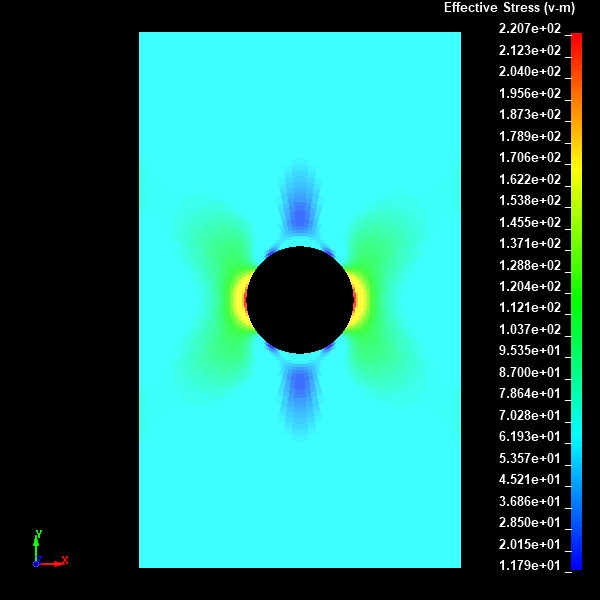
Fig.21 Case003のミーゼスの相当応力分布図(None表示)

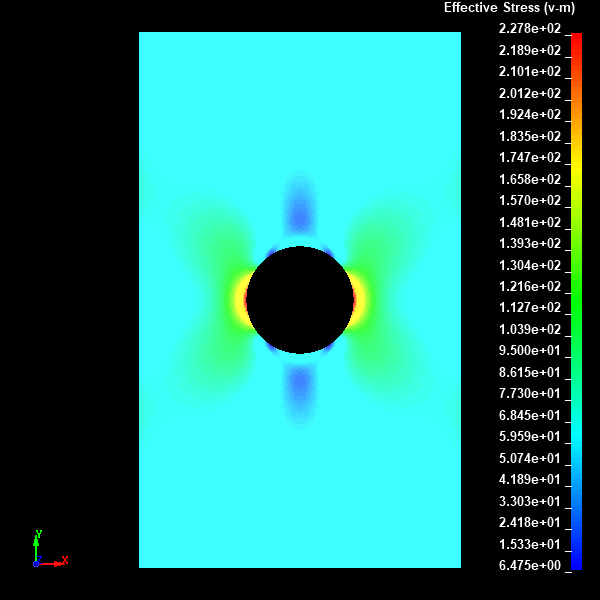
Fig.22 Case004のミーゼスの相当応力分布図(None表示)

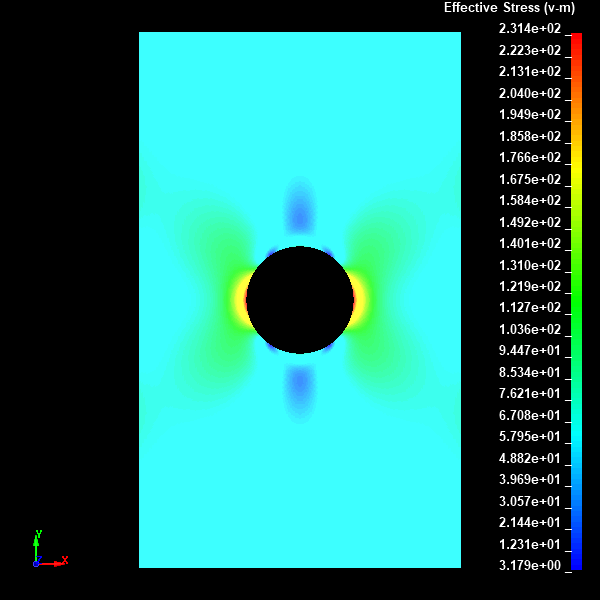
Fig.23 Case005のミーゼスの相当応力分布図(None表示)

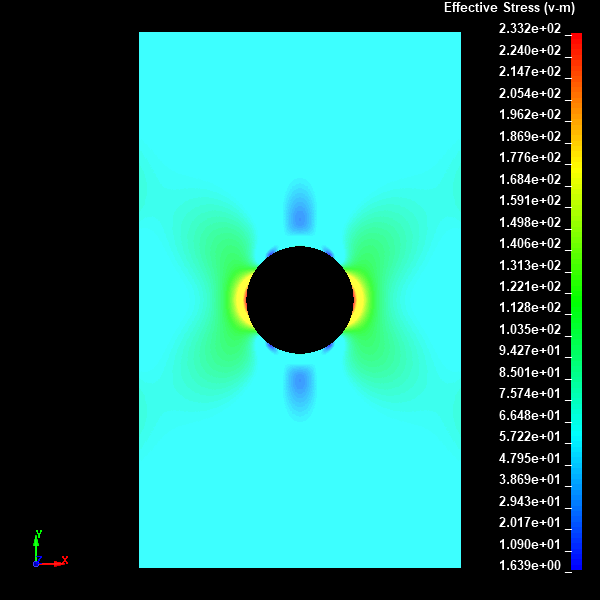
Fig.24 Case006のミーゼスの相当応力分布図(None表示)

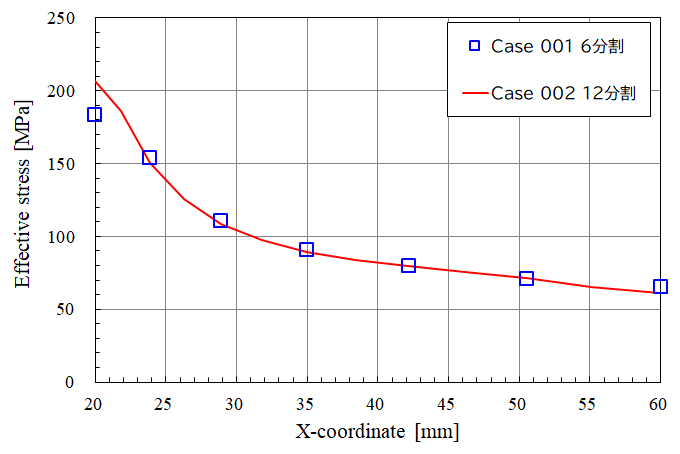
Fig.25 Case001とCase002のミーゼスの相当応力の比較

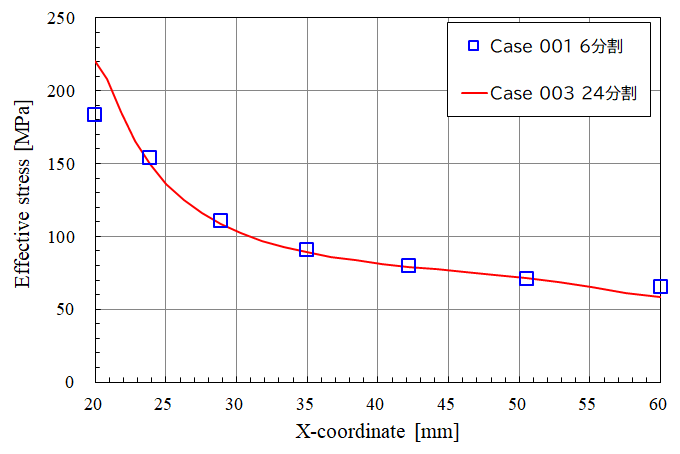
Fig.26 Case001とCase003のミーゼスの相当応力の比較

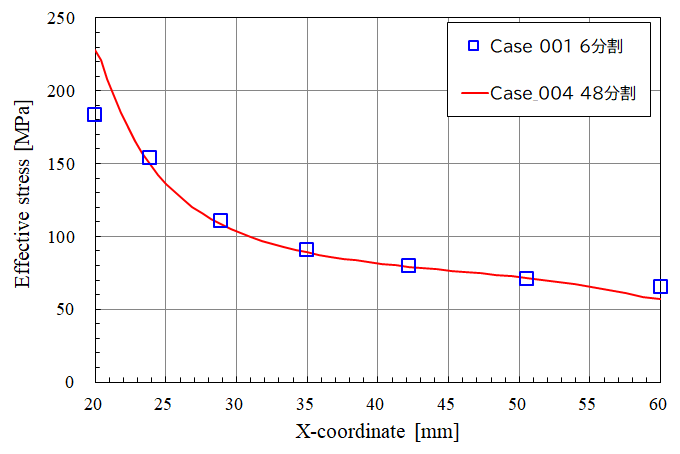
Fig.27 Case001とCase004のミーゼスの相当応力の比較

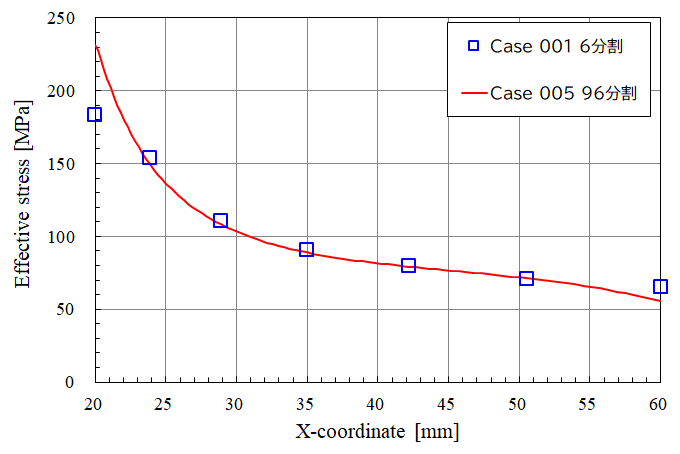
Fig.28 Case001とCase005のミーゼスの相当応力の比較

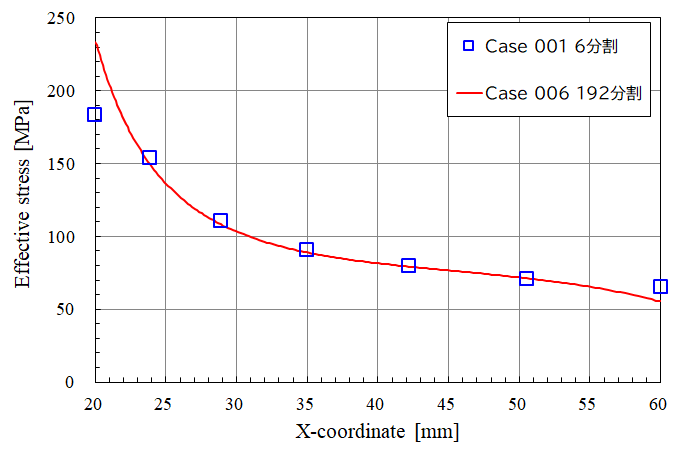
Fig.29 Case001とCase006のミーゼスの相当応力の比較

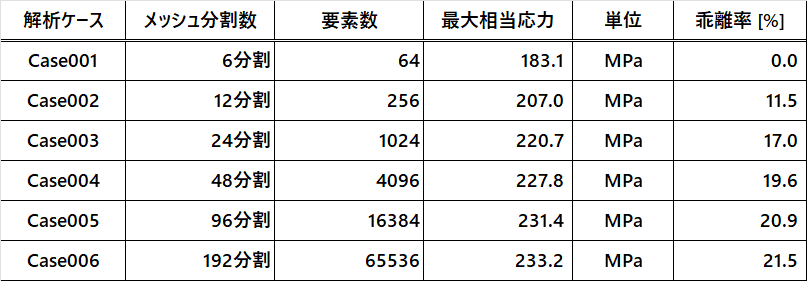
Table.1 解析ケースと相当応力の最大値の一覧表