株式会社ランスモアのホームページへようこそ。

No.429 Non-linear buckling analysis of thin-walled cylinder being subjected to axial compressive load

例題283 Buckling mode analysis で参考にした論文で検討された圧縮荷重を受けた薄肉円筒の非線形座屈解析をLS-DYNAの陰解法でシミュレーションしました。
Reference1：三原, 小林, 藤井：軸圧縮を受ける弾性円筒シェルの後座屈解析, 日本機械学会論文集(A編) 77巻776号(2011-4)
Reference2: Yamaki, N., elastic stability of circular cylindrical shells(1984), p.230, p.433, North-Holland.
解析条件：円筒の直径 D=200mm, 肉厚 t=0.247mm, 高さ H=113.9mm, ヤング率 E=5560MPa, ポアソン比 Nu=0.30
円筒の下端部を変位完全拘束し、上端部を下方向に圧縮させた際に円筒に生じる座屈変形挙動をLS-DYNAの陰解法機能を使用して解析しました。
円筒は初期は弾性座屈の臨界荷重に達すると座屈し急激に耐荷重が低下します。変形が進むと新たな座屈モードに次々と飛び移りながらシフトしていきます。

Keywords: Postbuckling Analysis, Non-Linear Implicit LS-DYNA, *Section_shell elform=10(BWC)

Tool: LS-PrePost ver.4.3, LS-DYNA SMP Double Precision R800 Win64

なお，本事例はサンプルであることをご了承下さい。

December-25-2015
June-16-2020 update

Fig.1 Disp=0.11mm, Load=791N

Fig.2 Disp=0.12mm, Load=453N

Fig.3 Disp=0.16mm, Load=492N

Fig.4 Disp=0.17mm, Load=466N

Fig.5 Disp=0.27mm, Load=570N

Fig.6 Disp=0.29mm, Load=404N

Fig.7 Disp=0.39mm, Load=402N

Fig.8 Disp=0.60mm, Load=317N

Fig.9 Disp=0.73mm, Load=341N

Fig.10 Disp=1.03mm, Load=296N

Fig.11 Disp=1.29mm, Load=281N

Fig.12 Disp=1.48mm, Load=282N

Fig.13 Disp=1.96mm, Load=309N

Fig.14 Disp=3.24mm, Load=251N

Fig.15 Disp=4.50mm, Load=237N

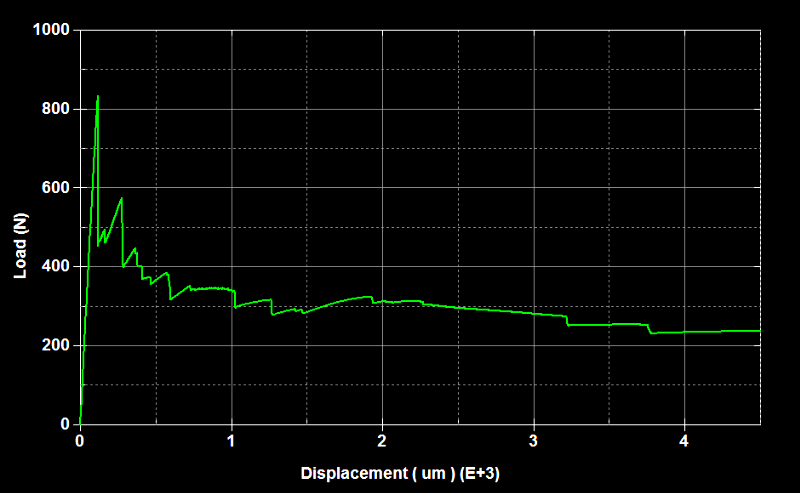
Fig.16 Graph X-Axis : Displacement (micro-meter), Y-Axis : Load (N)

Fig.17 Disp=0.11mm, Load=791N, Effective Stress

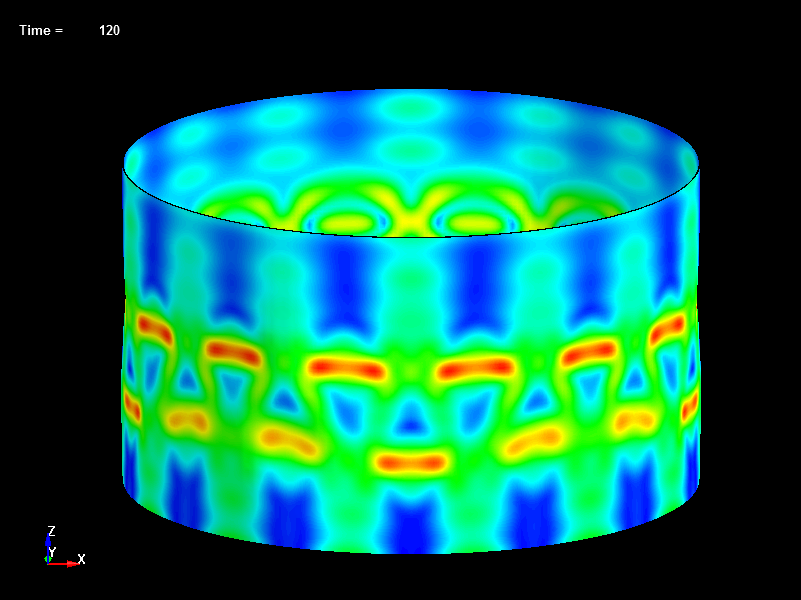
Fig.18 Disp=0.12mm, Load=453N, Effective Stress

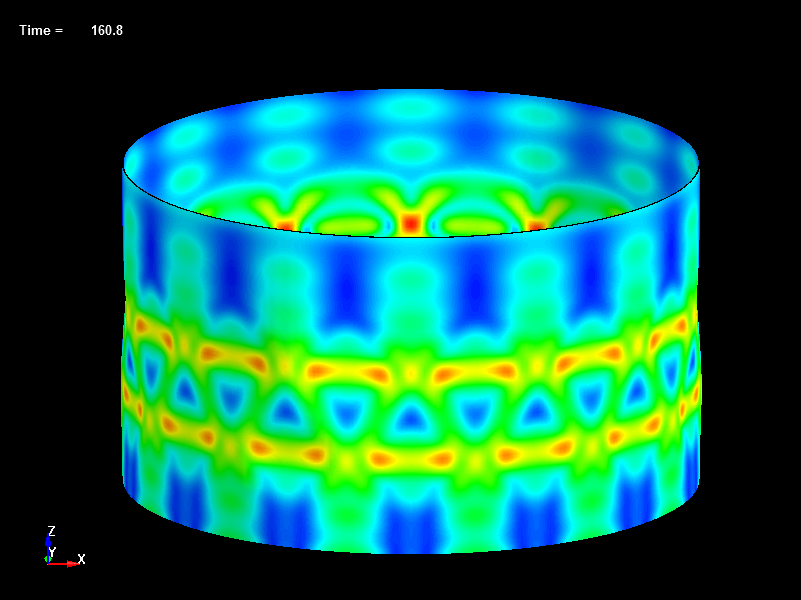
Fig.19 Disp=0.16mm, Load=492N, Effective Stress

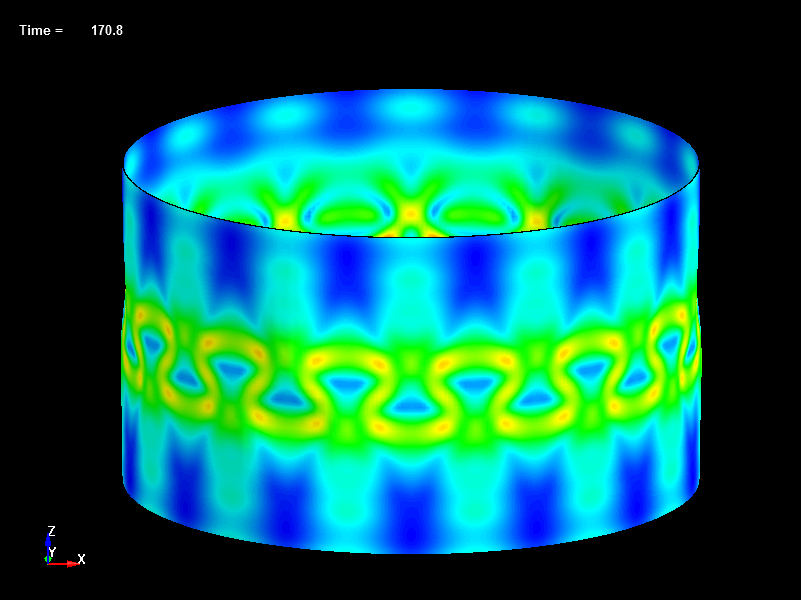
Fig.20 Disp=0.17mm, Load=466N, Effective Stress

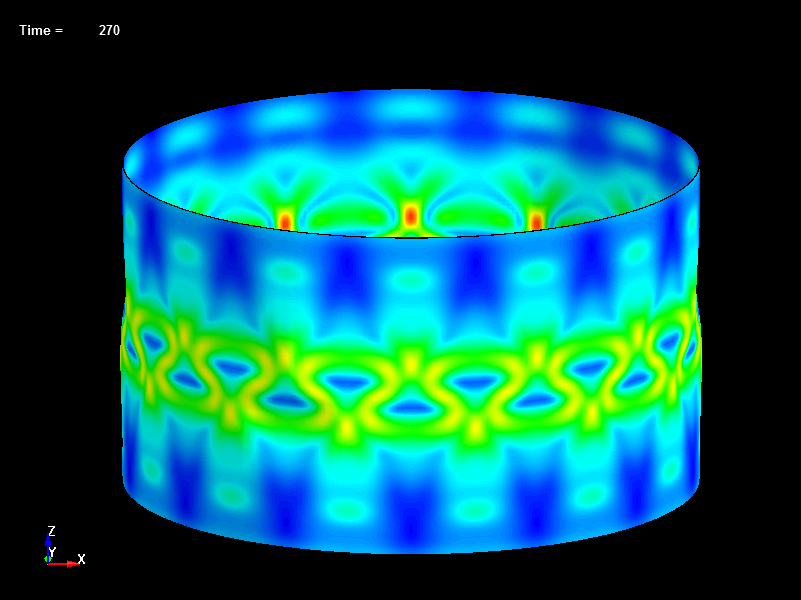
Fig.21 Disp=0.27mm, Load=570N, Effective Stress

Fig.22 Disp=0.29mm, Load=404N, Effective Stress

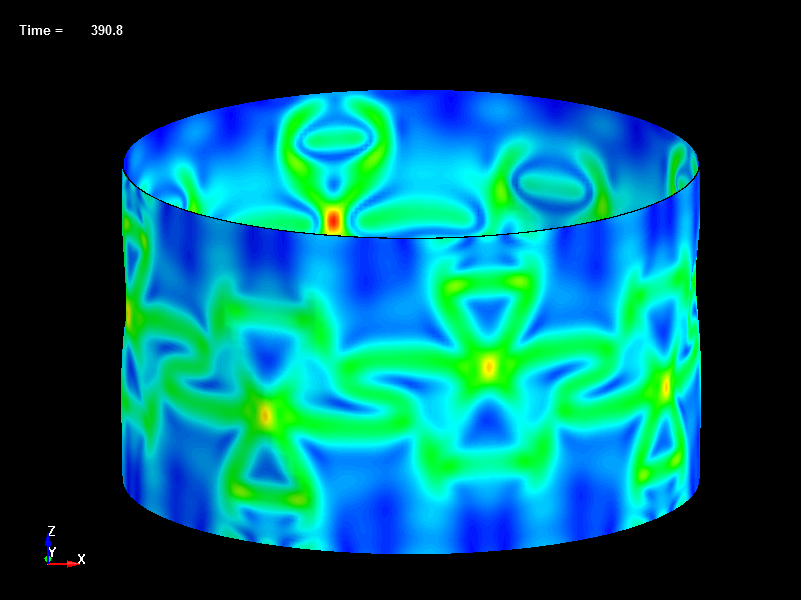
Fig.23 Disp=0.39mm, Load=402N, Effective Stress

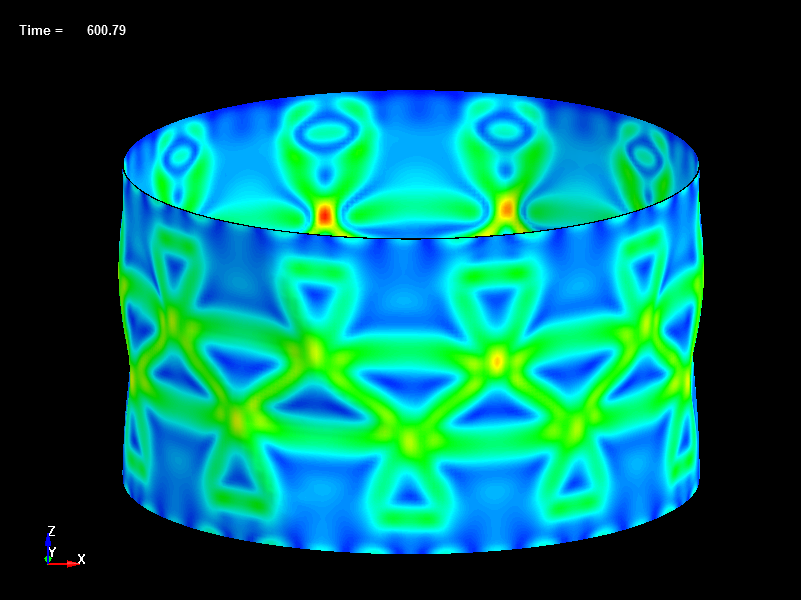
Fig.24 Disp=0.60mm, Load=317N, Effective Stress

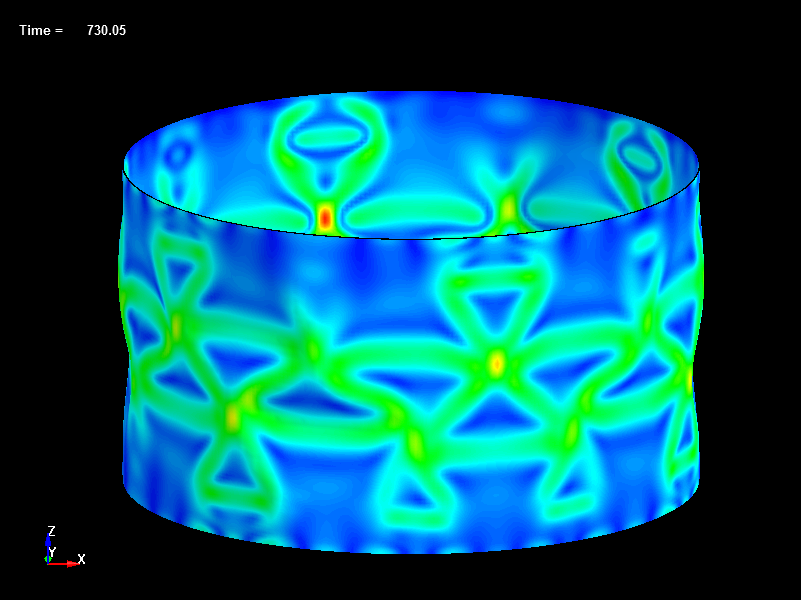
Fig.25 Disp=0.73mm, Load=341N, Effective Stress

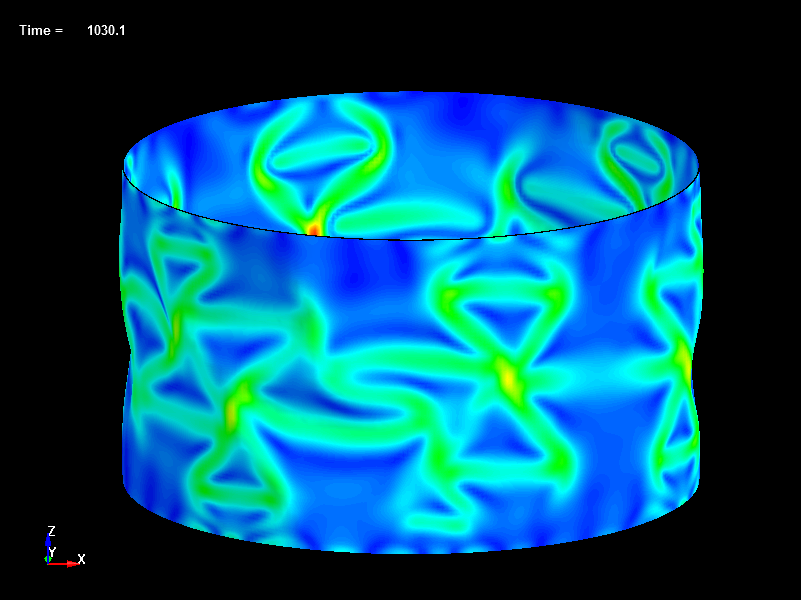
Fig.26 Disp=1.03mm, Load=296N, Effective Stress

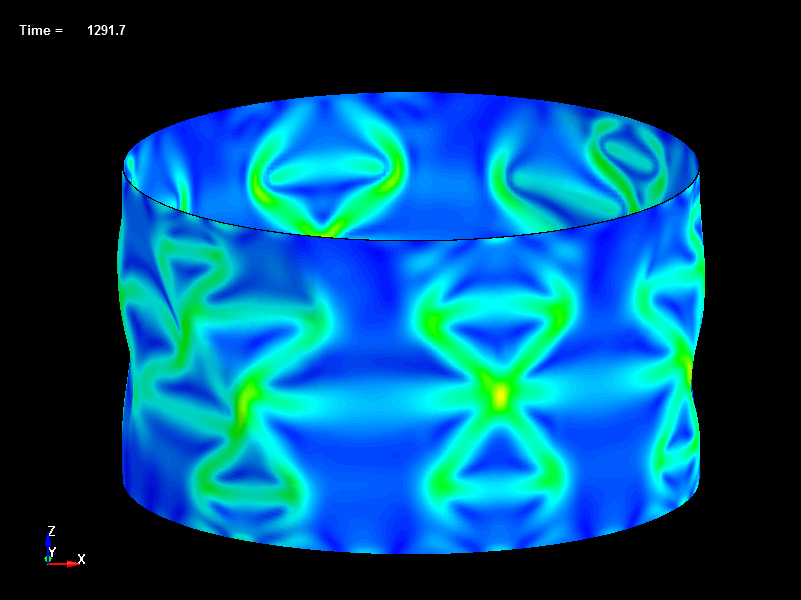
Fig.27 Disp=1.29mm, Load=281N, Effective Stress

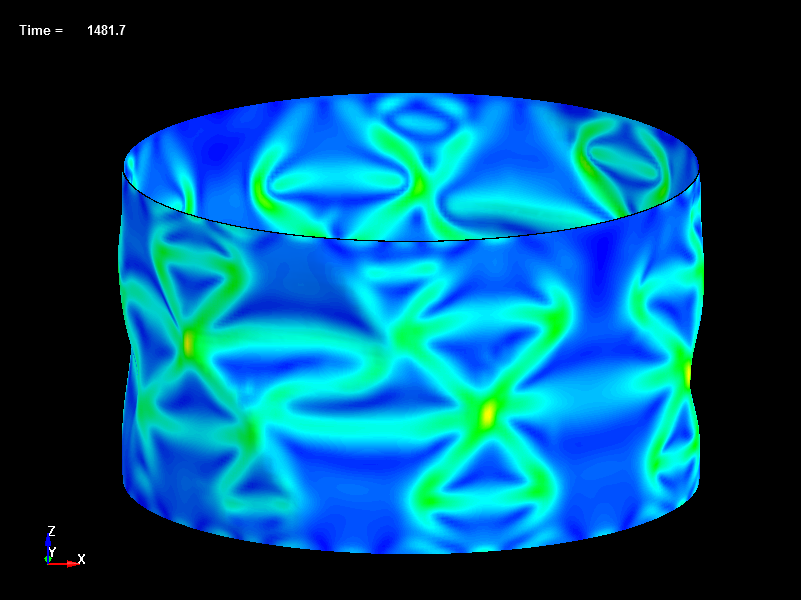
Fig.28 Disp=1.48mm, Load=282N, Effective Stress

Fig.29 Disp=1.96mm, Load=309N, Effective Stress

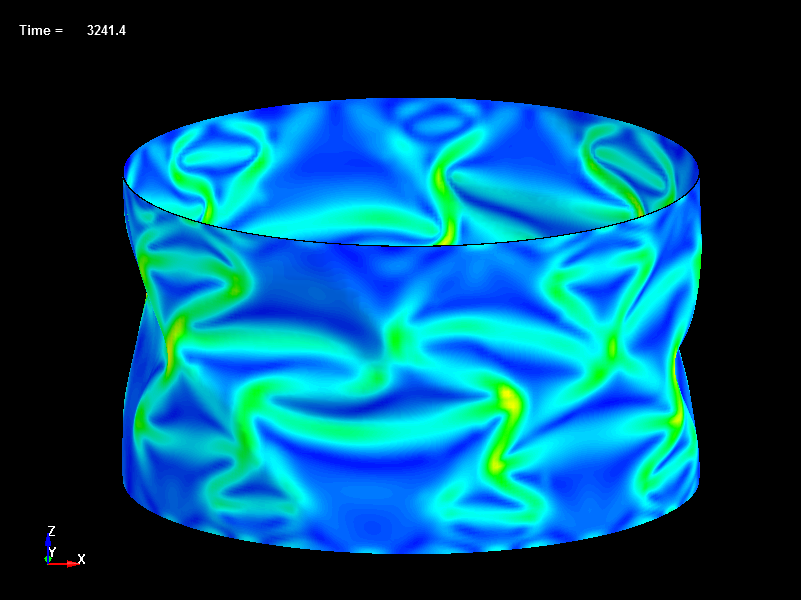
Fig.30 Disp=3.24mm, Load=251N, Effective Stress

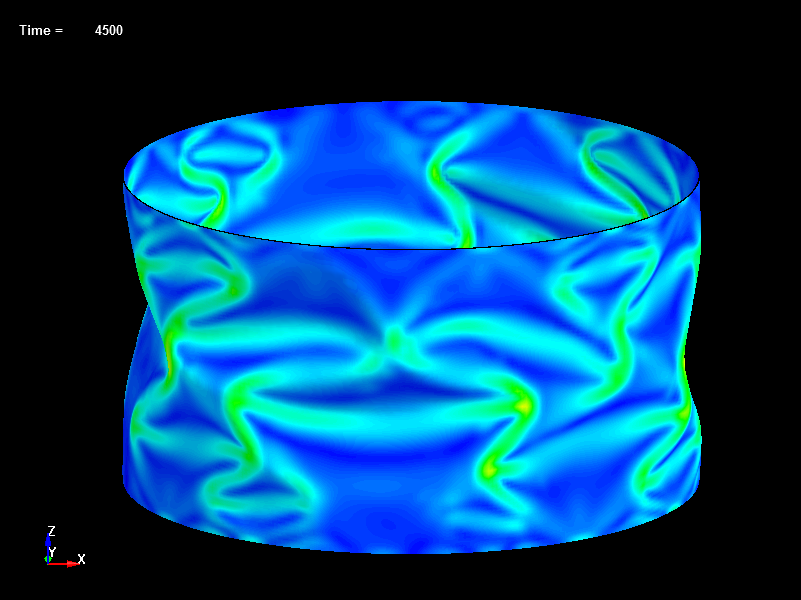
Fig.31 Disp=4.5mm, Load=237N, Effective Stress